You Can't Make Them Brighter

by Rick Scott

Did you know that when you look at a non-stellar object through a telescope that it's usually dimmer than looking at it with your naked eye? It's true, so why do telescopes make these object easily visible? The answer is the telescope makes them bigger, even if it makes them dimmer. This effect applies only to non-stellar or diffuse objects such as galaxies and nebulas or clusters where you can’t resolve the individual stars. Stellar objects behave differently which could be the subject of another article.

Most of the diffuse objects are so small your eye can't detect them because they don’t illuminate enough retinal cells in the eye. By making them bigger with a telescope or binoculars, you're allowing the image of the object to illuminate more retinal cells which makes the object visible. If you don't have a large enough telescope aperture the image of the object will never be as bright as the naked eye brightness. Here's how this works.

Let’s start with some basic information on how your eye works. Refer to the following drawings. The light enters the eye through the cornea and passes through the pupil which is the opening of the iris. The iris is a variable aperture opening that controls how much light enters the eye. The light is then focused by the lens to form a sharp image on the retina at the back of the eye. The cornea also helps in the job of focusing the light and it is this part of the eye that refractive eye surgery modifies to eliminate or minimize the need to use glasses.

The drawings on the left shows the eye with a large pupil opening which represents the eye at night or in a dark setting. The drawing on the right shows a small pupil opening which is appropriate for a day time setting or when looking at a very bright object at night such as the moon through a telescope. In both of these situations, the diameter of the pupil (aperture) determines how much light enters the eye. The dark adapted eye can have an aperture as large as 7mm (5mm when you get older) and is usually about 2mm when outside on a bright day. The two drawings show how the pupil size controls the size of the light beam entering the eye.

           

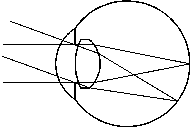
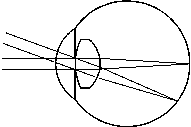
The drawings also show that light entering from any given direction as parallel rays is focused to a point at the back of the eye on the retina. Thus, the entire aperture is used for each point on the object we’re looking at. This is a critical idea so you can understand that the size of the beam of light entering the eye affects how bright the object appears. If you could force the size of the pupil to vary while looking at an object, you’d be able to vary how bright it looks. Now let’s see how this applies to using a telescope at night for dim deep-sky objects.

Imagine you're looking at the sky with your naked eye and your pupil opening is 7mm in diameter. Think of this as using a telescope with a magnification of 1X and an aperture of 7mm (0.276"). That’s a very small telescope! Now, let's assume that the object we want to look at requires 100X of magnification to make its image large enough to see detail and we’re using a scope with a 305mm (12") aperture. This aperture is referred to as the entrance pupil. A telescope with an eyepiece also has an exit pupil which is the ‘optical’ size of the opening at the observer end of the eyepiece. The exit pupil size is calculated by dividing the aperture of the telescope (entrance pupil) by the magnification it's being used at. For this example, 305mm divided by 100 is equal to 3.05mm which is less than half of the eye’s dark adapted pupil of 7mm. This is effectively the same as having the eye's pupil only opening to 3.05mm!

As previously seen in the drawings, the brightness of the image is affected by the size of the entering beam of light. The telescope’s exit pupil does the same thing by limiting the size of the beam of light to the size of its exit pupil. In the last example, the size of the beam of light is 3.05mm which effectively stops the eye down to this size. The brightness is proportional to the cross-sectional area of the light beam, which varies as the square of the diameter. In other words, a light beam that is two times larger in diameter will be four times brighter. In the previous example, if the exit pupil could be increased to 7mm, the image of the object will be 7^2 / 3.05^2 = 49 / 9.3025 = 5.27 times (or 1.75 magnitudes) brighter.

We could use the equation that we used to calculate the exit pupil backwards to find the telescope aperture necessary to achieve a 7mm exit pupil with a magnification of 100X. To do this, multiply the exit pupil by the magnification to find the desired aperture. So, 7mm times 100 is equal to 700mm (27.6"). Wouldn’t we all like to have such a large telescope!

Ok, so now we all own 27.6" telescopes, but what if we wanted to make the object bigger now by cranking up the magnification some more. Let's say we push the magnification up to 150X so we could see some more detail. Now the exit pupil is 700mm divided by 150 to give us an exit pupil of 4.67mm. So now our object is bigger, but it’s a little dimmer, but still brighter than we had with the 12" scope. We could go through the same exercise as before and find that we now need a 1050mm (41.3") telescope. Of course we are now in a size range that most of us wouldn’t even consider, so we’ll just have to accept the slightly dimmer image of the object. The difference in this case is only 2.27 times or 0.9 magnitudes.

So far I’ve only showed you how to size the scope for a given magnification to achieve the same brightness as the naked eye. What happens if we make the scope bigger than that to try to make it even brighter? Let’s use the example of 100X magnification and use the 200" Hale telescope at the Palomar Observatory which has an aperture of 5080mm. The exit pupil is 5080 divided by 100 which is equal to 50.8mm. Now that’s a large light beam and a lot of light! The only problem is that our eye has an aperture of 7mm and only that much of this 50.8mm light beam can get in. Our own pupil effectively stops this large telescope to 700mm, so the image is not any brighter than in the 27.6" telescope and no brighter than the naked eye view!!

Actually, the situation is worse than it seems. If the 200" Hale telescope were a refractor we’d be done with our calculations, but it isn’t. Reflecting telescopes usually have some sort of central obstruction we have to deal with. I don’t know what the central obstruction of the Hale scope is, but let’s use a small obstruction of 15% of the diameter of the scope which is 762mm or 30". The size of the obstruction in the exit pupil is calculated the same way as the size of the exit pupil itself. It will also have the same percent of obstruction in the exit pupil, so 15% of 50.8mm is 7.62mm. In this case, the obstruction is larger than our eye’s pupil so no light will get through and we don’t see anything. If we want to use the Hale scope to best advantage, we should use a magnification that produces a 7mm exit pupil. This magnification is found by dividing the telescope aperture by the exit pupil to give, 5080mm divided by 7mm, which equals 726X.

So why do we build such large telescopes? Well, they’re not used for visual observing. The cameras and other instruments normally used have entrance pupils large enough so they don’t limit the telescope and can take advantage of the large aperture. The instruments are designed for the scopes they’re used on and the designers take the characteristics of the telescope in mind while in the design phase.

Even in amateur size telescopes, the size of the central obstruction in the exit pupil needs to be accounted for. If it gets large compared to the pupil of the eye, it will block the light from the central part of the eye and make observing difficult. Some of you have probably seen this when using low magnifications to observe the moon or when trying to use the scope in the day time. The bright object or lighting causes the eye to stop down so the central obstruction is a larger percentage of the eye’s pupil.

The bottom line is that you just can’t make an dim astronomical object appear any brighter than with the naked eye. You can make it easier to see by making it bigger and maximize how bright you can see it by using a telescope with the right size aperture.